Коло і круг
Круг — геометрична фігура, яка складається з усіх точок площини, відстань від яких до даної точки не перевищує заданої. Ця точка – центр круга. Радіус – задана відстань. Радіус, хорда і діаметр кола є радіусом, хордою та діаметром відповідного кругу.Площою круга називається границя послідовності площ правильних багатокутників, вписаних в дане коло, при необмеженому збільшенні кількості сторін. Площа круга обчислюється за формулою:

Довжина кола 
Об'єм кулі:
Коло
Коло — геометричне місце точок площини, відстань від яких до заданої точки, що називається центром кола, є постійною величиною і дорівнює радіусу кола.
Термінологія
Внутрішню частину кола, тобто геометричне місце точок, віддаль яких до центра кола не перевищує радіус, називають кругом.Відрізок прямої, що сполучає дві точки кола називається хордою. Найдовша з хорд, діаметр, проходить через центр кола. Діаметр кола дорівнює двом радіусам.Пряма може не мати з колом спільних точок, мати з колом одну спільну точку (така пряма називається дотичною до кола) або мати з ним дві спільні точки (така пряма називається січною до кола).Дотична до кола завжди перпендикулярна до її діаметра, один з кінців якого є точкою дотику

Хорда, січна, дотична, діаметр.

Дуга, сектор та сегмент
Дві точки на колі розбивають коло на дві дуги. Кут між двома радіусами, проведеними до двох точок на колі, називається центральним. Область круга, обмежена двома радіусами й дугою називається сектором кола. Область круга, обмежена хордою та дугою, називається сегментом.
Довжина кола і площа круга
Довжину дуги кола з радіусом R, утвореного центральним кутом , виміряним у радіанах, можна обчислити за формулою
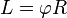
Довжину кола з радіусом R можна обчислити за формулою

де π — число пі, яке визначається як відношення довжини кола до його діаметра.Площа обмеженого колом круга дорівнює

де D = 2R — діаметр.Упродовж багатьох століть математиків цікавила задача про квадратуру кола: побудову за допомогою лінійки та циркуля квадрату з площею, що дорівнювала б площі круга. Ця задача не має розв'язку, оскільки число пі трансцедентне, що довів у 1882 Фердинанд фон Ліндеманн.
Дотичні і нормалі
Рівняння дотичної до кола в точці 

де A, B і С — коефіцієнти в загальному рівнянні кола.Рівняння нормалі в цій же точці можна записати як

